PC5252
Week 13
Review + Hints.
Week 12 Artificial neural networks
Missed the previous lecture...
Neural networks have a very large degree of freedom, which makes them prone to overfitting with limited training data. Some techniques to deal with overfitting:
- Weight decay: Essentially suppression of hidden layer weights using either an L1 or L2 norm
- Early stopping: Return the network parameters when the validation loss is minimum
- Dropout: Randomly setting weights to zero at each iteration (seen as regularization, i.e. lowering of instantaneous capacity to reduce overfitting)
- Data augmentation: Augmenting training data with simple transformations of data which the network should be invariant to, e.g. translations/scaling/rotation)
Beyond multilayer perceptrons
- Autoencoders:
- Learning of representation $$ z\in\mathbb{R}^m$$ for data $$x\in\mathbb{R}^n$$, by attempting to generate recreated data $$\hat{x}\in\mathbb{R}^n$$ from $$z$$.
- Undercomplete autoencoders ($$m<n$$) are trained using a simple loss function penalizing discrepancy between $$x$$ and $$\hat{x}$$. A linear decoder and L2 loss, results in learning principal components in PCA.
- Overcomplete autoencoders ($$m\ge{}n$$) typically learn the identity function, but can be trained to learn useful representations.
- Convolutional neural networks (CNN):
- Essentially a convolutional layer, which implements (1) convolution with a kernel, i.e. cross-correlation, (2) non-linear activation, (3) downsampling by pooling of (possibly overlapping) subsets.
- Termed convolution because (1) rotation doesn't really matter, and (2) flipping the kernel results in nice formal properties for proofs.
- Recurrent neural networks (RNN):
- Modelling of dependencies between any point in the sequence, by using a hidden layer $$h$$ that is also set up as a sequence.
- The affine transformations (i.e. $$(W_1,W_2,W_3)$$) are kept constant across all location to keep the network small.
- Many variants, e.g. long short-term memory by learning when to forget dependencies.
$$$$ \hat{y}^{(t)} = \sigma_1\left( W_1h^{(t)} + B_1 \right), \quad{} h^{(t)} = \sigma_2\left( W_2x^{(t)} + W_3h^{(t-1)} + B_2 \right) $$$$
Week 11 Generalized Linear Models
(pg.238-249)
We consider the generalized linear model
$$$$ \hat{Y} := f^{-1}(Xw) = E[Y|X] $$$$
where $$f$$ is the link function (identity $$f$$ means the model is a general linear model).
Minimizing squared error with identity link is equivalent to maximizing the conditional probability under the normal model
$$$$ p(Y|X) = N(Y|Xw, \sigma^2 I) $$$$
Performing derivatives,
\begin{align*} \ln p(Y|X) &= -\frac{1}{2\sigma^2} |Y-Xw|^2 + \text{const.} \end{align*}
We find that the maximum wrt $$w$$ is essentially the L2 loss, while the maximum wrt $$\sigma^2 $$ is at $$\hat{\sigma}^2 = \frac{1}{N} | Y-X\hat{w} | ^2 $$.
We can generalize the model by choosing link functions $$f$$ that are possibly non-linear, e.g. probit or logit links, and consider again the minimization:
$$$$ L(Y,\hat{Y}) := -\ln p(Y|\hat{Y}(X)) $$$$
where we parametrize by the mean $$\hat{Y} = E[Y|X]$$ (the analogy would be the mean as an estimator of the normal model). In practice, we only need to fit the mean $$E[Y|X]$$ (instead of considering the full probability distribution), so the choice of $$f$$ is more for practicality.
We can always rephrase the general linear model in the Bayesian framework, and solve it in that framework (e.g. the final regression model is specified by the MAP estimate, or even by analytical methods).
$$$$ L(\theta|X,Y) = p(Y|X,\theta) = N(Y|X\theta_1, \theta_2 I) $$$$
Kernel methods
Consider the generalized design matrix,
\begin{align*} \Phi := \begin{pmatrix} \phi(x_1) \\ \vdots{} \\ \phi(x_n) \end{pmatrix} \equiv \phi(X) \end{align*}
$$\phi: \mathbb{R}^n \rightarrow \mathbb{R}^d$$ here is called a feature map (i.e. $$\phi(x) = (x^2,x,1)$$ for quadratic regression). Some new notation: $$\hat{Y}(X) = \Phi(\hat{w})$$ (training) and $$\hat{y}(x_*) = \phi_*^T\hat{w}$$ (evaluation).
Deriving $$\hat{w} = \Phi^T(\Phi\Phi^T)^{-1}Y := \Phi^T \tilde{Y}$$
Solution is to left-multiply by $$\Phi^T \Phi$$,
\begin{align*} \hat{w} &:= (\Phi^T \Phi)^{-1} \Phi^T Y \\ &= (\Phi^T \Phi)^{-1} \Phi^T (\Phi \Phi^T) (\Phi \Phi^T)^{-1} Y \\ &= (\Phi^T \Phi)^{-1} (\Phi^T \Phi) \Phi^T (\Phi \Phi^T)^{-1} Y \\ &= \Phi^T (\Phi \Phi^T)^{-1} Y \end{align*}
For any data point, we thus can write in terms of $$k$$,
$$$$ \hat{y}(x_*) = \phi_*^T \Phi^T \tilde{Y} = \sum_i^N \phi_*^T \phi_i \tilde{y}_i := \sum_i^N k(x_*,x_i) \tilde{y}_i = [k(x_*,x_i)]^T \tilde{Y} $$$$
and we also have,
$$$$ \tilde{Y} := (\Phi \Phi^T)^{-1} Y = [\phi_i^T \phi_j]^{-1} Y = [k(x_i,x_j)]^{-1} Y $$$$
This means, as opposed to defining the feature map $$\phi$$, evaluate it for $$x_*$$, then apply the linear transformation $$\hat{w}$$, for the kernel method we only need to evaluate $$k$$ for each of the $$N$$ rows before using them as weights for $$\tilde{y}_i$$. Note there was no need to explicitly choose the set of features which is needed to choose an appropriate feature map $$\phi$$ (although kernel methods scale poorly with training set size $$N$$).
More generally, any valid inner product on the feature space (codomain of $$\phi$$) is a valid kernel, and this can have arbitrary dimensions (i.e. infinite-dim Hilbert space). For the least-squares method, the kernel is explicitly the Euclidean inner product of the features of $$x$$.
Feature map equivalents
Since the inner product must be a positive squared-norm, the kernel $$k(x,x') = xx' - 1$$ is not a valid kernel, i.e. $$k(0,0) = -1 < 0$$.
Consider instead the Gaussian kernel, where we expand the middle term using Taylor expansion,
\begin{align*} k(x,x') &= \exp(-(x-x')^2/2) \\ &= \exp(-x^2/2) \exp(xx') \exp(-x'^2/2) \\ &= \exp(-x^2/2) \left(1 + xx' + \frac{1}{2}(xx')^2 + \ldots{}\right)\exp(-x'^2/2) \\ &= \exp(-x^2/2) \left(1,x,\sqrt{\frac{1}{2}}x^2,\ldots{}\right)^T \left(1,x',\sqrt{\frac{1}{2}}x'^2,\ldots{}\right)^T\exp(-x'^2/2) \\ &\equiv{} \phi(x)^T\phi(x')^T \end{align*}
We can use Mercer's theorem, which states the inner product is valid if the kernel is positive semi-definite (PSD), i.e. for any set of vectors $$\{x_1, \ldots{},x_N\} \in \mathbb{R}^n$$ the matrix $$K = [k(x_i,x_j)]$$ is PSD, where K is symmetric and has non-zero eigenvalues (i.e. $$z^TKz\ge{} 0 \forall{} z\in \mathbb{R}^N$$). We rely on the fact that the set of all PSD kernels is closed under addition $$k_i+k_j$$, multiplication $$k_ik_j$$, limits $$\lim_{i\rightarrow{}\infty} k_i$$, to obtain derivative kernels. Some common kernels,
- Linear: $$k = x^Tx'$$ (inner product by definition)
- Constant: $$k = c \ge{} 0$$ (which gives $$\quad{} K = c\mathbb{1}$$ which is PSD)
- Polynomial: $$k = (x^Tx' + c)^p$$
- Gaussian: $$k = \exp(-c|x-x'|^2)$$
Support Vector Machines
(pg.250-267)
SVMs are nice since they are sparse models, which help with poor N-scaling problem during model evaluation. We first consider the simplest SVM, i.e. linear binary classifier that maps $$ x \in \mathbb{R}^n \rightarrow y \in \{-1,1\}$$. The linear function is $$ x^T w + b $$, whose level sets are (n-1)-dimensional hyperplanes in $$\mathbb{R}^n$$.
The problem is formulated as finding a hyperplane that cleanly separates the data of different labels, i.e. we want to find model parameters $$w,b$$ such that $$ x_i^T w + b \le{} -1 $$ if $$y_i = -1$$, and $$ x_i^T w + b \ge{} 1 $$ if $$y_i = 1$$.
Margin between two hyperplanes
Consider two vectors $$x_+$$ and $$x_-$$ that each lie on the hyperplanes. The component $$w$$ is a vector normal to the hyperplane, so the distance (margin) between the two hyperplanes are:
$$$$ d = (x_+ - x_-) \cdot{} \hat{w} = (x_+ - x_-) \cdot{} \frac{w}{|w|} $$$$
Since at the margins, $$x_+ \cdot{} w = 1 - b$$ and vice versa, we finally have,
$$$$ d = 2/|w| $$$$
The optimization is thus $$ \max_{w,b} 2/|w|^2, \, y_i (x_i^T w + b) \ge{} 1$$ (hard margin, i.e. all data points fall outside the margin). By construction, the hyperplanes will pass through some data points $$x_i$$ (termed support vectors), and the central bisector $$x^T w + b = 0$$ is the maximum-margin hyperplane, which also defines the final model:
$$$$ \hat{y}(x_*) := \sgn(x_*^T \hat{w} + \hat{b}) $$$$
More generally, the linear transformation is the feature map $$\phi(x)^T w' + b$$, and we can use the kernel formulation as usual. Optimization with respect to N inequality constraints uses Lagrangian multipliers $$\mu$$, with additional constraints (dual feasibility, complementary slackness). This constrained optimization problem is known as the Karush-Kuhn-Tucker (KKT) conditions.
Blah blah blah. Importantly, the model is sparse, since $$\hat{\mu}_i$$ will be zero for any $$x_i$$ that is not a support vector, i.e. model evaluation only requires the support vectors. The dual optimization problem is a quadratic function in $$\mu$$, which is more efficiently solved than the primal problem.
Gaussian Process Regression
For more Bayesian approaches, i.e. with probabilities baked in and priors as hyperparameters, GPR is an alternative kernel-based method. GPR models are generally not sparse. The main focus is generating the posterior predictive distribution to make a probabilistic prediction $$p(\hat{y} | x_*,X,Y)$$ (rather than the usual point prediction).
The likelihood is in terms of the data features $$\Phi{X}$$, with the variance as a hyperparameter (i.e. iid errors):
$$$$ L(\theta|X,Y) = N(Y|\Phi{}\theta,\sigma_n^2I) $$$$
Using a conjugate normal prior $$\pi(\theta) = N(0,\Sigma_\pi)$$, we can obtain the posterior and posterior predictive distributions, the latter is,
$$$$ p(\hat{y} | x_*, X,Y) = N(\hat{y} | \sigma_n^{-2} \phi_*^T A^{-1} \Phi^T Y, \phi_*^T A^{-1} \phi_*) $$$$
where $$A := \sigma_n^{-2} \Phi^T \Phi + \Sigma_\pi^{-1} $$ is the posterior precision. We can further reparameterize by solving Eq. 250 (by left multiplying with A and right multiplying with $$(K + \sigma_n^2 I)$$), to factorize into separate kernels (covariances).
Bottomline: GPR is the Bayesian solution to the regression problem (learning problem over priors, as opposed to an optimization problem). It is also thusly named for its alternative formulation as a stochastic process. This method of doing regression is nice because it gives error estimates that also vary based on how far the prediction is away from the available dataset.
Week 10 Regression
(pg.216-237)
Regression involves constructing a map from data x to target y, i.e. $$\mathbb{R}^n \rightarrow \mathbb{R}^m$$.
Regression is not exactly classification with a continuous codomain ($$y|x$$ is a continuous distribution, as opposed to categorical RVs in classification), but can be extended from classification techniques since the conditional distribution is already specified by the model (whether implicit and/or non-parametric). Interpolation on the other hand can be seen as a specific application of regression, but is usually non-probabilistic.
Linear regression
In ordinary linear least squares, each data point x is an n-vector whose components are termed regressors. The corresponding target $$y$$ is scalar, and is termed the response (in the context of $$y(x)$$ or $$y|x$$). The regression model is simply,
$$$$ \hat{y}(x) := w\cdot{}x $$$$
describing an n-dimensional hyperplane $$\mathbb{R}^n\times{}\mathbb{R}$$, with $$n>1$$ known as multiple linear regression. For a training set $$\{(x,y)_i\}$$ of size $$N$$, we define the $$N\times{}(n+1)$$ design matrix,
\begin{align*} X:=\begin{pmatrix} x_1 & 1 \\ \vdots{} & \vdots{} \\ x_N & 1 \\ \end{pmatrix} \end{align*}
with the N-vector output,
$$$$ \hat{Y}(X) := Xw $$$$
The loss function is given as the residual sum of squares $$L(Y,\hat{Y}) := |Y-\hat{Y}|^2$$, known as the L2 loss in machine learning, and this has a simple analytical solution due to the model's linearity.
Analytical minimization of loss function
\begin{align*} L &= |Y-Xw|^2 \\ &= (Y-Xw)^T(Y-Xw) \\ &= Y^TY - 2(w^TX^TY) + w^TX^TXw \\ \partial_w L &= -2X^TY + 2X^TXw \\ \end{align*}
Thus $$L(Y,\hat{Y})$$ is minimized when $$w=(X^TX)^{-1} X^TY$$. Note the Gram matrix $$X^TX$$ is invertible when $$X$$ has full rank, i.e. the columns are linearly independent with $$N\ge{}n+1$$, or in other words, the regressors should not be perfectly correlated. In the case of an ill-conditioned $$X^TX$$, we can perform additional data transformations.
Ordinary least squares assumes the residuals $$y_i-\hat{y}_i$$ are iid normal RV with zero mean (error covariance proportional to identity). We can generalize this further:
- Weighted least squares with independent errors of different variances.
- Generalized least squares with errors following a general covariance matrix $$\Sigma$$.
This leads to the general solution,
$$$$ w = (X^T\Sigma^{-1}X)^{-1}X^T\Sigma^{-1}Y $$$$
Goodness of fit
Two common summary statistics for goodness-of-fit tests for linear least squares: (1) coefficient of determination, (2) reduced chi-squared statistic.
$$$$ R^2 := 1- \frac{|Y-\hat{Y}|^2}{|Y-\bar{Y}|^2} $$$$
This is interpreted as the proportion of Y variation that can be predicted by relationship with X. $$\hat{Y} = Y$$ gives exact fit and $$\hat{Y} = \bar{Y} $$ (Y mean) gives bad fit.
$$$$ \chi^2_{\nu} := \frac{1}{\nu} [Y-\hat{Y}]^T W [Y - \hat{Y}] $$$$
Overfitting when less than 1; underfitting when more than 1. Since errors are usually unspecified a priori, the chi-squared statistic can be used as a posteriori estimate of error variance.
Note again that a better analysis is always direct visualisation of residuals (i.e. $$Y-\hat{Y}$$) or quantile-quantile (Q-Q) plots (i.e. a quantile is the value of x such that area under curve on domain less than x has given area, or in other words the CDF of the probability distribution).
- Q-Q plots for linear least squares, we usually assume normally distributed residues. We can plot the quantiles of the fit, as well as the residuals which should roughly hover about the fit consistent with a normal distribution.
Ignore this fallacy, and you run the risk of reaching a wrong conclusion from simply using summary test statistics, e.g. the Anscombe's quartet (sharing near-identical summary statistics but are qualitatively different),
or the Datasaurus Dozen:
General linear models
Extensions of the linear model are available, e.g. polynomial regression. These are linear with respect to its parameters $$w$$ (and not the regressors, e.g. for quadratic regression the design matrix X is $$(x^2,x,1)$$).
- Multivariate linear regression: Target is vector-valued.
- Polynomial regression: Regressors are higher-ordered.
- Other basis regressions, e.g. Fourier basis $$\{e^{ijx}\}$$, or radial bases
Regularisation can also be done for linear least squares. Important since the Gram matrix becomes poorly conditioned as the dimensionality of the dataset increases (more data points => data points are similar to one another => columns becomes almost proportional => X is not necessarily full rank => Gram matrix becomes near-singular). This also results in large variances in model parameters w (overfitting).
One method of regularisation is ridge regression, which penalises large components of w, where $$\lambda{} $$ is typically used as a tunable hyperparameter:
$$$$ L'(Y,\hat{Y}) := |Y - \hat{Y}|^2 + \lambda{}|w|^2 $$$$
Minimization of $$L'(Y,\hat{Y})$$
$$$$ w = (X^TX + \lambda{}I)^{-1}X^TY $$$$
\begin{align*} \partial_w |Y-\hat{Y}|^2 &= -2X^TY + X^TXw \\ \partial_w \lambda|w|^2 &= 2\lambda I w \\ \end{align*}
Regularisation effectively makes the eigenvalues not particularly close to zero. Other regularisation methods include lasso regression that uses the L1-norm instead of the squared L2-norm, which tends to make w sparse (i.e. components for some regressors go close to zero, so we can choose which regressors to use).
Week 9.2 Classification
Logistic regression
This is essentially the simplest binary classifier. We consider the affine transformation $$ x \mapsto{} Wx + b $$, which we further fold $$b$$ into $$W$$ by augmenting $$x$$ with a constant unit component:
\begin{align*} x \mapsto{} w\cdot{}(x\oplus{}1) = \begin{pmatrix} w_1 \\ \vdots{} \\ w_n \\ b \end{pmatrix} \cdot{} \begin{pmatrix} x_1 \\ \vdots{} \\ x_n \\ 1 \end{pmatrix} \end{align*}
We can use the logistic (expit) function $$\sigma(x)$$ to map the output into [0,1] for a probabilistic representation (i.e. $$\hat{y} \in [(1,0), (0,1)])$$:
$$$$ \sigma (x) := \frac{1}{1+e^{-x}} = \frac{1}{2}\left(1+ \tanh\frac{x}{2}\right) $$$$
This finally yields the logit model,
$$$$ \hat{y}(x) := (\sigma{}(w\cdot{}x), \sigma{}(-w\cdot{}x)) $$$$
We optimize (i.e. minimize) the KL divergence over the model parameters $$w$$, which describes the discrepancy between the probability distributions of $$y$$ and $$\hat{y}$$, where $$L(y,\hat{y})$$ is known as the cross-entropy loss for classification,
$$$$ D_\text{KL}(y,\hat{y}) = -\sum_i y_i \ln\hat{y}_i + \text{const.} \equiv{} L(y,\hat{y})+ \text{const.} $$$$
We can show that $$L(y,\hat{y})$$ is minimized when $$y = \hat{y}$$, so we numerically optimize for $$\min_w\{y_1 - \sigma(w\cdot{}x)\}$$
Multiclass classification
The logit model for binary classification, under a suitable transformation, can be written more explicitly in the following form with $$k=2$$,
$$$$ \hat{y}(x) = \left( \frac{e^{w_1\cdot{}x}}{\sum_i^k e^{w_i\cdot{}x}} , \ldots{}, \frac{e^{w_2\cdot{}x}}{\sum_i^k e^{w_i\cdot{}x}} \right) $$$$
This is known as the softmax function, i.e. a smooth approximation to the hard argmax function, $$\text{argmax}(w_1\cdot{}x,\ldots{},w_k\cdot{}x) = (0,\ldots{},0,1,0,\ldots{},1)$$. The cross-entropy loss function has the same form as that of the binary classifier. The overall accuracy is generally examined mainly from the generalized confusion matrix.
Other classifiers include the k-neighbour clustering and decision trees.
Clustering
Three broad classes on clustering algorithms:
- Centroid: Clustering of data points based on distance from a set of centroid points. While these points can be learnt, the number of clusters generally needs to be pre-determined.
- Density: Similar to centroid methods, but based on density of distribution instead, e.g. DBSCAN and OPTICS. The cutoff definition for the density-based criterion can be arbitrary.
- Connectivity: Based on how connected they are to one another (with respect to some distance metric). Powerful since they can be used to construct cluster hierarchies, but more computationally expensive.
k-means clustering is the archetypal centroid-based clustering, which finds a partition of data into k subsets such that the overall variance of all subsets is minimized. This is defined by the following loss function L for partition P over subsets of data set S, each with mean m,
$$$$ L(P) :=\sum_i^k \sum_{x\in{}S_i} |x-m_i|^2 = \sum_i^k |S_i| \text{Var}[S_i], \qquad{} P=\{S_1,\ldots{},S_k\} $$$$
One such optimization algorithm is the naive k-means, which is simple to implement and widely used. Can be extended with more robust techniques (e.g. to avoid high sensitivity to choice of initial means).
Naive k-means
- Choose a starting set of k means, $$\{m_1,\ldots{},m_k\}$$
- For each data point, determine the nearest mean point (with respect to Euclidean metric) and partition them into the same subset.
- Compute the new means and repeat.
Week 9.1 Machine learning
(pg.185-)
Introduction
Machine learning is essentially a set of specifications for four components:
- Dataset
- Model
- Objective function, e.g. loss/profit
- May not necessarily be obvious, e.g. overall cluster variances in clustering, or number of cuts edges in partitioning
- Optimization procedure
Some terminology notes:
- Unsupervised learning generally involves learning the probability distribution $$p(x)$$ of some data $$x$$, while supervised learning involves learning the conditional distribution $$p(y|x)$$ given an associated vector of labels $$y$$. Distinction not usually clear-cut since they can be rephrased arbitrarily.
- Parametric models have more rigid assumptions on model structure (e.g. normal approximation is parametric with $$(\mu,\sigma)$$), as opposed to non-parametric models (e.g. histograms (as a model) with flexibility in bin specifications). This differs from statistical modelling that uses the term to indicate a lack of assumed distribution or dependency on parameters.
- Hyperparameters refer to parameters that are tuned (and not necessarily learnt as in hierarchical models). This is typically done using a validation dataset, which is also used for monitoring for overfitting.
- Capacity indicates the degrees of freedom of the machine learning, which seeks to generalise well on data that has not been provided as experience (assuming training and test datasets are i.i.d.). Low capacity results in underfitting (large training error), and conversely a large capacity results in overfitting (large testing error relative to training).
- Bias and variance is another categorization for models, with underfitted models having high bias (lower accuracy for training data) and low variance (lower variability between similar data), and conversely for overfitted models. The central concern is regularization, i.e. reducing overfitting by modifying the objective function to encourage model simplicity (low variance).
- No free-lunch theorem states: "Any two algorithms have an equivalent average performance over all possible problems". In other words, machine learning (and optimization) is highly task-specific and not universal.
- Curse of dimensionality refers to the difficulty of generalizing to data with high dimensionality, since the number of possible configurations (and hence the amount of data required) increases exponentially.
Topics of choice to be covered in the remainder of the course: Clustering, Classification, Regression, Kernel methods, Artificial neural networks.
Representation learning
This addresses learning the appropriation representation of data, such as in clustering or dimensionality reduction. The prototypical dimensionality reduction method is principal component analysis (PCA), which projects the data distribution into the subset of dominant directions (forming the reduced representation) in the data space.
PCA algorithm
- Compute sample mean and thus the centered data $$X$$.
- Compute sample covariance $$S = X^TX/N$$ and its eigenvectors and eigenvalues.
- Determine the $$m$$ largest eigenvalues and form the $$n\times{}m$$ matrix $$U=[u_1,\ldots{},u_m]$$.
- Compute the reduced representation as the $$N\times{}m$$ matrix $$Z:=XU$$.
The singular value decomposition (SVD) is typically used for PCA to directly obtain $$Z$$ without computing $$S$$. Note also that PCA traditionally has many different names (e.g. Hotelling transform, Karhunen-Loeve transform, proper orthogonal decomposition) due to reinvention of the same idea in different fields.
PCA can also be used as a whitening transform such that the transformed data is uncorrelated and normalized (i.e. the sample covariance is the identity). This transformation is given by the following, where $$m=n$$ and $$\Lambda$$ is the diagonal eigenvalue matrix,
$$$$ W := \Lambda^{-1/2}U^T, \qquad{} \hat{X} := XW^T $$$$
As an aside, PCA is considered machine learning since (1) the objective function is the maximization of data variance after the projection onto a vector subset (and minimizes bias), and (2) it can be shown that the full and partial eigensystems of $$S$$ are already the optimal set of vectors of each $$m_i$$.
Binary classification
Classification is the supervised learning of a map from data $$x\in\mathbb{R}^n$$ to its target class $$y\in\{1,\ldots{},k\}$$ or, more generally, to a probability mass function $$p(y|x)\in[0,1]^k, \sum_i^k p_i = 1$$. Each training example $$x$$ has an associated target $$y$$ in one-hot form (which can be interpreted as the true probability mass function) of size $$k$$. The classification is binary if $$k=2$$.
The goal is to output a vector on the probability simplex such that $$\hat{y}(x) \approx y$$, without restricting to a one-hot form (soft classification). This, as opposed to hard classification, is more informative, especially when the classes are less distinct.
Week 7 Advanced sampling
(pg.118-132)
Slice sampling
Slice sampling has some adaptive aspects that can evolve between iterations. Basic idea is to uniformly cut the probability distribution into the top half, then sample uniformly from the line. The self-tuning aspect comes from refining the bound for sampling. See code below:
#!/usr/bin/env python3 """Slice sampling.""" import matplotlib.pyplot as plt import numpy as np import scipy def target(t): return np.exp(-0.5 * (t**4 - 3*t**2 - 2*t + 5)) chain = [1] chain_len = 10_000 step_size = 0.1 x = chain[0] while len(chain) < chain_len: # Sample a line along the probability axis u = scipy.stats.uniform.rvs(loc=0, scale=target(x), size=1) # Find interval for distribution falling above this line, approximation interval = [x-step_size, x+step_size] while target(interval[0]) > u: interval[0] -= step_size while target(interval[1]) > u: interval[1] += step_size # Attempt to sample from approximated interval while True: x = scipy.stats.uniform.rvs(loc=interval[0], scale=interval[1]-interval[0], size=1)[0] if target(x) > u: break # If below distribution, refine interval bound and retry interval[int(abs(interval[1]-x) < abs(interval[0]-x))] = x chain.append(x) # Plot plt.subplots(figsize=(6,2)) ts = np.linspace(-3, 3, 1001) plt.plot(ts, target(ts)) plt.hist(chain, bins=100, range=(-3, 3), density=True) plt.show()
Hamiltonian MC sampling
seed = theta0
for step in range(num_steps):
Need to use a symplectic (leapfrog is one simple implementation) integrator, to update the value of $$\theta$$, see above.
The scale of the parameters (position and momentum) should be roughly equivalent to that of
Tip
Is it disingenuous to suggest HMC is more efficient, when more steps are taken as well. What really is the goal of all these adaptive protocols, is it to increase acceptance rate and large dimensionality?
There are also extensions to HMC for more adaptability. Note that if one follows the Hamiltonian exactly, the trajectory of motion is closed, so one can implement a NUTS (no U-turn strategy), e.g. early evolution termination once a U-turn is detected.
#!/usr/bin/env python3
"""Hamiltonian Monte-Carlo sampling."""
import numpy as np
def gradlogtarget(x):
pass
def leapfrog(x0, p0, step_size, steps):
x = x0
p = p0
p += step_size/2 * gradlogtarget(x) # initial momentum update
for _ in range(steps):
x += step_size * p
p += step_size * gradlogtarget(x)
p -= step_size/2 * gradlogtarget(x) # final momentum correction
return (x, p)
def target(x):
pass
chains = [
[(1,1)],
[(1,2)],
]
chain_len = 100_000
step_size = 0.05
steps = 20
for chain in chains:
x = chain[0]
for _ in range(chain_len):
p = np.random.normal(0, 1, 2)
xprop, pprop = leapfrog(x, p, step_size, steps)
if target(xprop, pprop) /
# Acceptance rate is relatively high, roughly 0.65 for 2D.
https://chi-feng.github.io/mcmc-demo/app.html?algorithm=HamiltonianMC&target=multimodal
Adaptive proposals
Basic idea is to modify the proposal kernel in a way that is informed by the current state of the chain, or the state of the ensemble of chains.
Other examples include simulated annealing (analogous to the Boltzmann distribution with temperature T), where the temperature scale is slowly reduced according to some schedule.
$$$$ p_i(\theta) \propto{} p(\theta)^{(1/T_i)} $$$$
Week 6.1 Other MCMC sampling
(pg.109-117)
Choice of proposal kernel should be easy to sample from, and sufficiently tuneable (balance between high acceptance, vs low informativity). Note some other subtelities:
- Chain should be burned in, by discarding initial samples which is more largely correlated with the initial starting point.
- Use of multiple chains good for parallelism, and having distributed set of points over the whole parameter space.
- Diagnostics performed by looking at "marginal chains" for a single parameter.
MCMC diagnostics
There are several metrics to characterize chains:
- Potential scale reduction factor (PSRF): Estimate of how much the sample variances might reduce if the chains run to infinity.
- Autocorrelation duration and effective sample size. The main metric to look at is the first point at which the autocorrelation hits the zero crossing.
Chain optimality is characterized by the sampling efficiency (i.e. $$\tau_\theta = N_\text{eff}/N$$. Note that if the acceptance rates are either too high or too close, the sample efficiency is also minimal.
The optimal acceptance rate is roughly 0.44 for d=1 and 0.23 for d>5. The ESS again is a heuristic, and can be noisy for short chain lengths.
MCMC diagnostic tests
Given the same target distribution used in the previous sampling strategies. Note the histogram of values from high/low variance used in proposal distribution, with higher variances resulting in noisier data, and lower variances resulting in localized data.
The plots for stdev = 0.1 and 10 look similar to that of the optimal stdev parameter for the proposal distribution (i.e. 1). The measure of stationarity/mixing, as well as sampling efficiency shows otherwise:
Plot of sample values over sample index, which shows the degree of mixing between samples. Stationarity is added as a metric by halving the partial chains used, and both stationarity and mixing are identified by the PSRF value (see code for explanation):
Autocorrelation graphs for measure of sampling efficiency (by calculating the average sampling delay between approximately independent samples):
Gibbs sampling
Gibbs sampling
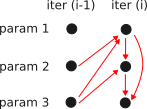
Let the joint distribution be $$p(\theta_1,\theta_2,\theta_3)$$. The first iteration sample is given by the following step-wise updates:
\begin{align*} \theta_{1;1} &\sim p(\cdot{}|\theta_{0;2},\theta_{0;3}) \\ \theta_{1;2} &\sim p(\cdot{}|\theta_{1;1},\theta_{0;3}) \\ \theta_{1;3} &\sim p(\cdot{}|\theta_{1;1},\theta_{1;2}) \end{align*}
#!/usr/bin/env python3 """Gibbs sampling of normal model with unknown mean and variance.""" def mposterior1(t2): N, S1, S2 = 10, 0.15, 0.55 sqrtc = np.sqrt(t2/N) return np.random.normal(loc=S1, scale=sqrtc) def mposterior2(t1): N, S1, S2 = 10, 0.15, 0.55 tau2 = (N-1)*S2/N + (S1-t1)**2 df = N return 1/np.random.chisquare(df=df) * tau2 * N # Gibbs sampling num_samples = 20_000 size_burnin = 10_000 size_skip = 100 def gibbs_sampling(point): # Perform burn-in to randomize 'point' seed for i in range(size_burnin): t2 = point[1] t1prop = mposterior1(t2) t2prop = mposterior2(t1prop) point = (t1prop, t2prop) # Perform Gibbs sampling and accept every 'size_skip' point points = [point] for i in range(num_samples): for j in range(size_skip): t2 = point[1] t1prop = mposterior1(t2) t2prop = mposterior2(t1prop) point = (t1prop, t2prop) points.append(point) return points # Perform Gibbs sampling for two initial seeds points1 = gibbs_sampling((0.5,0.5)) points2 = gibbs_sampling((0.5,1))
Blocked Gibbs sampling
Parameters can be additionally partitioned into blocks (usually groups of parameters that are more strongly correlated with each other), so that Metropolis-Hastings can be used for sampling within each parameter block.
Week 5.2 Markov chains
(pg.103-108)
A Markov chain is a sequence of random variables $$ \{\theta_i\} $$ where the probability distribution of each $$\theta_i$$ depends only on $$\theta_{i-1}$$, in other words:
$$$$ p(\theta_i|\theta_{j<i}) = p(\theta_i | \theta_{i-1}) $$$$
We focus on chains for which there exists a unique stationary distribution $$p_S$$. Stationarity is guaranteed by the condition of detailed balance, i.e. the probability of transitioning to $$\theta'$$ from $$\theta$$ is the same for the opposite direction,
$$$$ p_T(\theta'|\theta)p_S(\theta) = p_T(\theta|\theta')p_S(\theta') $$$$
where $$p_T$$ denotes the transition probability between states $$\{\theta_i\}$$. We use this idea for Markov Chain Monte Carlo (MCMC) sampling, whose stationary distribution is the target distribution $$p_S = p$$, in order to perform more efficient sampling from general high-dimensional distributions.
Metropolis-Hastings algorithm
The Metropolis-Hastings algorithm is typically used as a basis/framework for more advanced Markov Chain Monte Carlo (MCMC) sampling. The algorithm uses proposal distributions $$q$$ (similar to rejection sampling) that differ depending on the current state of the chain, $$ \theta \sim{} q(\cdot{}|\theta) $$. We denote $$q(\cdot{}|\cdot{})$$ as the proposal kernel (which takes in a distribution and outputs another distribution).
#!/usr/bin/env python3 """Metropolis-Hastings sampling.""" import matplotlib.pyplot as plt import numpy as np def f(t): return np.exp(-0.5 * (t**4 - 3*t**2 - 2*t + 5)) def proposal(x, sqrtc=0.1): return np.random.normal(x, sqrtc) # tuning parameter, sqrtc x0 = 1 # initial seed chainlen = 100_000 # Initialize chain x = x0 chain = [x] acceptance_prob = np.random.uniform(size=chainlen) # Metropolis-Hastings algorithm for p in acceptance_prob: xprop = proposal_point(x, sqrtc) if p < f(xprop)/f(x): x = xprop chain.append(x) xs = np.linspace(-2, 3, 10000) ys = f(xs) plt.plot(xs, ys, label="Target") plt.hist(chain, bins=50, density=True, linewidth=1, label=f"Result (seed={x0})") plt.legend() plt.show()
Week 5.1 Sampling methods
(pg.93-102)
Inverse transform sampling
This is a direct sampling method that performs a transformation from the uniform distribution to the target distribution. Note that this is only applicable to one-parameter distributions.
#!/usr/bin/env python3 """Inverse transform sampling.""" import matplotlib.pyplot as plt import numpy as np def f(t): return np.exp(-0.5 * (t**4 - 3*t**2 - 2*t + 5)) xs = np.linspace(-3, 3, 1000) ys = f(xs) # Compute the CDF cdf = np.cumsum(f(xs)) / np.sum(f(xs)) # Random sampling of uniform distribution xs_sampled = np.random.uniform(0, 1, size=10000) ys_sampled = np.interp(xs_sampled, cdf, xs) # interpolate with cdf(xs) plt.plot(xs, ys, label="Target") plt.hist(ys_sampled, bins=50, density=True, label="Result") plt.show()
Rejection sampling
In the naive implementation, for every point we sample a pair of uniformly-distributed random numbers $$(a,b)$$, where $$ a \in{} [0,1]$$ and $$b$$ falls within the support of the distribution. We accept $$b$$ only if $$a$$ falls below the volume of the target distribution $$q$$. Code below:
#!/usr/bin/env python3 """Rejection sampling.""" import matplotlib.pyplot as plt import numpy as np def f(t): return np.exp(-0.5 * (t**4 - 3*t**2 - 2*t + 5)) xs = np.linspace(-3, 3, 1000) # Sample according to proposal distribution # Here, naively, is the uniform distribution xs_sampled_raw = np.linspace(-3, 3, 10000) selection_prob = np.random.uniform(0, 1, 10000) # Choose points that fall under the target distribution # Divided by 1 because the proposal (uniform) distribution is 1 everywhere xs_sampled = xs_sampled_raw[selection_prob <= f(xs_sampled_raw)/1] plt.plot(xs, f(xs)) plt.hist(xs_sampled, bins=50, density=True) plt.show()
The sampling can be made much more efficient by selecting a proposal distribution (which does not necessarily need to be normalized) that aligns better to the target distribution, i.e. $$ q \gtrapprox p $$. This is alternatively seen as rejecting points $$(\theta_i, q(\theta_i)u_i)$$ (which will always fall within the volume $$q$$ since $$ u \in [0,1]$$) lying above the volume $$p$$.
Importance sampling
Similar to rejection sampling, but we weight the samples accordingly, instead of rejecting them.
$$$$ E_p[\tau] = \int{} \,d\theta \tau(\theta) q(\theta) \frac{p(\theta)}{q(\theta)} = E_q[\tau{} w] \approx \frac{\sum_i^N \tau(\theta_i) w_i}{\sum_i^N w_i} $$$$
where the weights $$w_i = w(\theta_i) := \frac{p(\theta_i)}{q(\theta_i)} $$.
#!/usr/bin/env python3 """Importance sampling.""" import matplotlib.pyplot as plt import numpy as np def f(t): return np.exp(-0.5 * (t**4 - 3*t**2 - 2*t + 5)) xs = np.linspace(-3, 3, 1000) # Sample according to proposal distribution # Here, naively, is the uniform distribution xs_sampled = np.linspace(-3, 3, 10000) xs_weights = f(xs_sampled)/1 # divide by q(xs) if using a better proposal distribution q xs_weights_normalized = xs_weights / np.sum(xs_weights) print("Expectation:", np.sum(xs_sampled * xs_weights_normalized)) # Expectation: 0.9765235307434326 plt.plot(xs, f(xs)) plt.hist(xs_sampled, bins=50, density=True, weights=xs_weights_normalized) plt.show()
Note that we can use an evenly-spaced Cartesian grid, since the end goal is not to draw random samples, but to compute expectations. This is much more generalizable than rejection sampling, but still inefficient in high dimensions.
We can compare their effective sample size (ESS) across different sampling methods:
- Inverse transform sampling: $$N_{eff} = N$$, but the sampling process is inefficient
- Rejection sampling: $$N_{eff}$$ is the number of accepted samples
- Importance sampling: Only the subset of larger weights significantly contribute to information about the target distribution. A heuristic for estimating ESS is $$N_{eff} = 1/\sum_i^N \hat{w}_i^2$$, where $$\hat{w}$$ are the normalized weights.
We can easily see how this is related to the variance of the sampled weights:
$$$$ N_{eff} = \frac{1}{N\langle{}\hat{w}^2\rangle{}} = \frac{1}{N\cdot{}\text{Var}[\hat{w}] + 1/N} $$$$
Note that a high/low ESS does not imply high/low convergence to the target distribution.
We cna
Week 4.2 Monte Carlo Sampling
(pg.86-92)
Sampling is important for both visualization and estimation of non-standard posterior distributions. Visualization for higher-dimensions can be achieved by looking at marginal densities, e.g. a five-parameter distribution summarized by a triangle of plots for its two-parameter marginals:
$$$$ p(\theta_1,\theta_2) \propto \sum_{\theta_3}\sum_{\theta_4}\sum_{\theta_5} p(\theta_1,...\theta_5) $$$$
Calculation of expectations on the other hand will require proper normalization, but is relatively trivial since the normalization is simply the sum of values (because the volume occupied by each point in a Cartesian grid is equal).
Week 4.1 Exchangeability
(pg.70-85)
Exchangeability condition
Let $$x_i$$ denote the outcome of the i-th trial. The trials are identical and independently distributed (iid) if:
$$$$ p(x_i) = p(x_j),\quad{} j\neq i $$$$
while they are exchangeable if:
$$$$ p(x_i, x_j) = p(x_j, x_i) $$$$
Denoting $$\theta_i$$ as the outcome probability of each group of trials, and $$x_{ij}$$ the outcome of each trial (i.e. belonging to the group $$i$$). Trials can be made exchangeable:
- $$x_{ij}$$ are exchangeable, or if covariates $$k_{ij}$$ exist, then $$x_{ij}|k_{ij}$$ are exchangeable
- If differences between trials can affect the data:
- If no information to distinguish particular trials, then $$ x_k $$ are not exchangeable, but $$ \theta_i $$ and $$x_{ij}|\theta_i$$ are => hierarchical model
- If information is available to distinguish trials, $$ x_k $$ and $$\theta_i$$ are not exchangeable, but $$x_{ij}|\theta_i$$ are, and we can similarly add covariates to turn it into an exchangeable hierarchical model
This yields the following relation for the joint posterior, with the relation without the hyperparameter for comparison,
\begin{align*} p(\theta|x) &\propto{} p(x|\theta) p(\theta) = L(\theta|x) \pi(\theta) \\ p(\theta,\phi|x) &\propto p(x|\theta,\phi) p(\theta,\phi) = L(\theta|x) \pi(\theta|\phi) p(\phi) \end{align*}
Note that the likelihood is not a function of $$\phi$$ since it depends on $$\phi$$ only through $$\theta$$, i.e. $$\phi$$ is the hyperparameter that informs the prior.
Beta-binomial distribution
Let $$x_i \sim \text{Bin}(n=10, \theta_i) $$, and $$\theta_i \sim \text{Beta}(a,b)$$, with the following hyperprior
Week 3.2 Multinomial distribution
(pg.58-69)
Posterior derivation only requires proportionality
The common expression used when evaluating the posterior distribution is:
\begin{align*} p(\theta|x) \propto{} L(\theta|x) \pi{}(\theta) \end{align*}
where we aim to estimate the estimand $$\theta$$. Since the form of the posterior distribution is dependent only on $$\theta$$, only the $$\theta$$ terms need to be concluded, with the normalization factor fixed after identifying the distribution the posterior is similar to. For example, the following form:
\begin{align*} f(\theta) \propto{} \theta{}^\alpha{} (1-\theta)^{\beta} \end{align*}
must imply the following normalization constant:
\begin{align*} f(\theta) = \frac{\Gamma(\alpha+\beta-2)}{\Gamma(\alpha-1)\Gamma(\beta-1)} \theta^\alpha (1-\theta)^\beta \end{align*}
Week 3.1 Multi-parameter models
(pg.45-57)
Multi-parameter models allow for estimation of multiple parameters at the same time.
We can perform marginalisation to narrow the size of unknown parameters for visualization, e.g. if the parameters to marginalize over are measurement noise. The relation is as per definition of marginal distributions,
$$$$ p(\theta{}_1|x) = \int{} d\theta{}_2 \;p(\theta{}_1, \theta{}_2 | x) $$$$
which states that sampling from the joint posterior $$p(\theta{}_1,\theta{}_2|x)$$ usually provides the direct/only way of computing the marginal posterior.
Suppose we have the two-parameter normal distribution, the joint likelihood given n observations of $$x_i$$ is the following, which we can rewrite in terms of the sufficient statistics $$s_1$$ (sample mean) and $$s_2$$ (unbiased sample variance, i.e. over n-1),
\begin{align} L(\theta{}_1,\theta{}_2|x) &\propto{} \theta_2^{-n/2} \exp{}\left( -\frac{1}{2} \frac{\sum_i^n (x_i - \theta{}_1)^2}{\theta{}_2} \right) \\ &\propto{} \theta_2^{-n/2} \exp{}\left( -\frac{1}{2} \frac{(n-1)s_2 + n(s_1 - \theta{}_1)^2}{\theta{}_2} \right) \end{align}
We can visualize this by assigning the following improper joint prior $$\pi{}(\theta_1,\theta{}_2) \propto{}\theta{}_2^{-1}$$, and plot contour plots of the resulting (proper) posterior (log-density) distribution. Below, the sufficient statistics $$(s_1,s_2)$$ are (0.15,0.55) and (0.07, 1.04) on the left and right respectively, and the x marks the correct mean and variance (of the standard normal). We see that the bias and uncertainty is larger with a smaller data set.
This leads directly into a sampling method faster than sampling from the joint distribution itself, by decomposing the joint posterior into the conditional and its marginal, i.e. we sample $$\theta_2$$, then sample $$\theta_1$$ from the corresponding conditional distribution (known $$\theta_2$$ with constant prior for $$\theta_1$$), see below,
$$$$ p(\theta{}_1,\theta{}_2|x) = p(\theta{}_1|\theta{}_2,x)p(\theta_2|x) $$$$
The multiple-observation posterior with known $$\sigma^2$$ and improper constant prior $$\sigma_0^2 \rightarrow \infty$$ is given as
$$$$ p(\theta|x) = N\left(\theta{}\middle| \frac{s(x)}{n}, \frac{\sigma^2}{n}\right), \qquad s(x) = \sum_i^n x_i $$$$
which we can use to derive
$$$$ p(\theta_1|\theta_2,x) = N\left(\theta_1\middle|s_1,\frac{\theta_2}{n}\right) $$$$
The marginal posterior on the other hand is obtained by integrating the joint posterior over $$\theta_1$$, i.e.
\begin{align} p(\theta_2|x) &\propto \theta_2^{-(n+1)/2} \exp{\left(-\frac{(n-1)s_2}{2\theta_2}\right)} \\ \theta_2|x &\sim{} \text{Inv-}\chi{}_{n-1}^2(s_2) \end{align}
This reduces the sampling of the two-parameter joint distribution, to an initial sampling of the \text{Inv-}\chi{}^2 distribution to obtain $$\theta_2$$ candidates, with which we use to sample from $$N$$.
Week 2.2 Normal distribution
(pg.37-44)
The Gaussian distribution is given by,
$$$$ N(x|\mu{},\sigma{}^2) = \frac{1}{\sqrt{2\pi{}\sigma{}^2}} \exp{\left(-\frac{(x-\mu)^2}{2\sigma{}^2} \right)} $$$$
For a known $$\sigma{}^2$$ (and $$\mu\equiv\theta$$), the likelihood (and thus the conjugate prior) has a Gaussian form,
$$$$ L(\theta|x) \propto \exp{\left( -\frac{(\theta-x)^2}{2\sigma{}^2} \right)},\qquad{}\pi{}(\theta) = N(\theta{}|\mu_0,\sigma_0^2) \propto \exp\left(-\frac{(\theta{} - \mu_0)^2}{2\sigma_0^2}\right) $$$$
which yields the posterior (hint: by completing the square),
$$$$ p(\theta{}|x) = N(\theta{}|\mu_1,\sigma_1^2),\qquad{} \frac{1}{\sigma_1^2} = \frac{1}{\sigma^2} + \frac{1}{\sigma_0^2},\quad{} \frac{\mu_1}{\sigma_1^2} = \frac{x}{\sigma{}^2} + \frac{\mu_0}{\sigma_0^2} $$$$
Tip
When computing posteriors and/or likelihoods, one strategy for evaluation is to discard all terms that do not depend on the variables in their distribution.
The inverse variance (of the normal distribution) $$1/\sigma^2$$ is known as precision, which is the sum of the likelihood and prior precisions, while the mean is the precision-weight average of the corresponding means.
The posterior predictive distribution of observation $$\tilde{x}$$ is
$$$$ p(\tilde{x}|x) = N(\tilde{x}|\mu_1, \sigma^2 + \sigma_1^2) $$$$
Tip
The mean and variance identities (in the forward direction) are pretty useful for computing the corresponding for the overall distribution.
We can further derive the posterior distribution for multiple-observation data $$\{x_i\}$$, left out from this text.
Sufficient statistic
A sufficient statistic is some function of the data that is sufficient to provide information on the parameter we want to estimate, e.g. $$s(x)$$ for the Gaussian distribution is the sum of the observations.
Other models
Note that if the Gaussian distribution has a known mean but unknown variance, then the likelihood is not a Gaussian distribution, but is instead,
$$$$ L(\theta{}|x) \propto{} \theta{}^{(-\frac{n}{2})} \exp{\left(-\frac{s(x)}{2\theta}\right)},\qquad{} s(x) = \sum_i^n(x_i-\mu)^2 $$$$
$$$$ \pi(\theta) = \text{Inv-Gamma}(\theta|a,b) \propto{} \theta{}^{-(a+b)} \exp{\left(-\frac{b}{\theta}\right)} $$$$
For the Poisson distribution, we also have,
$$$$ L(\theta|x) \propto{} \theta^{s(x)} \exp(-n\theta),\qquad{} s(x) = \sum_i^n x_i $$$$
$$$$ \pi(\theta) = \text{Gamma}(\theta|a,b) \propto{} \theta^{(a-1)} \exp(-b\theta) $$$$
Week 2.1 One-parameter models
(pg.22-36)
We introduce a simple example to illustrate Bayesian modelling.
Example
Ball A thrown onto a table lands in a position with horizontal coordinate $$ \theta \in [0,1]$$. Ball B is thrown onto the table $$n$$ times and lands $$ x $$ times to the right of A. What is $$ P(\theta{} \in \Theta | x) $$ for some subinterval $$ \Theta{} \subset [0,1] $$?
The Binomial distribution, that can be used to describe the p.m.f. of the successes, is the forward probability model (aleatoric uncertainty). The corresponding likelihood function is the inversion of this forward model (epistemic uncertainty), and is continuous and unnormalized.
\begin{align} \text{Bin}(x|n,\theta{}) = \left(\begin{matrix}n\\x\end{matrix}\right) \theta{}^x (1-\theta)^{(n-x)} \end{align}
The normalization constant $$ \int_{[0,1]} d\theta{} L(\theta{}|x) $$ is the evidence Z for the given number of successes x. Assuming a uniform prior,
$$$$ \pi{}(\theta{}) = U(\theta{}|0,1) = 1_{[0,1]} (\theta{}) $$$$
we can write the marginal likelihood in terms of the beta function and its associated distribution,
\begin{align} B(a,b) &:= \int_0^1 dt\;t^{(a-1)} (1-t)^{(b-1)} = \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)},\qquad \Gamma(a):=\int_0^\infty{} dt\;t^{(a-1)}e^{-t} \end{align}
$$$$ \text{Beta}(t|a,b) = \frac{1}{B(a,b)}t^{(a-1)}(1-t)^{(b-1)} $$$$
Example 2.1
Show that the marginal distribution Z(x) is uniform on {0,...,n}, and find the posterior distribution.
Example 2.2
Between 1745 and 1770, there were 241945 females out of 493472 children born in Paris. What is the probability that the probability that any child is female is larger than 50%?
Laplace calculated this to be approximately $$ 10^{-42}$$, using similar Bayesian methods.
The frequentist method to this would be to calculate the mean and construct confidence intervals to derive the standard deviation. Then derive p-values for how many sigma the value is, i.e. $$ \sigma{}^2 = x\theta{}(1-\theta{}) $$.
Predictive distributions
Existing observations can be used to inform subsequent observations. Let $$ \tilde{x}\in \{0,1\} $$ be the outcome of another trial from the same population.
If the value of $$\theta{}$$ is known or assumed, the predictions have a known distribution (aleatoric uncertainty):
\begin{align} p(\tilde{x}|\theta{}) = \begin{cases} 1 - \theta{}, &\tilde{x} = 0 \\ \theta{}, &\tilde{x} = 1 \end{cases} \end{align}
However, when $$\theta$$ is unknown and no observations are made, the predictions are given by the prior predictive distribution (i.e. marginal likelihood). Conversely, with observed data, this yields the posterior predictive distribution.
Bayesian statistics can be used to answer non-frequentist questions, with the result making as much sense as the assumptions we lay upon it,
Example 2.3
Assuming the Earth is 1e12 days old, and we observe the sun rising every day since antiquity, and assuming a uniform prior, the probability of the sun rising tomorrow
$$$$ p(\tilde{x}|x) = \frac{x+1}{n+2} \approx{} 1 - 1e12 $$$$
This is a relatively small number; the use of a prior that is skewed towards 1 is more appropriate.
Choice of prior
The uniform prior U(0,1) is commonly used since it often simplifies calculations and imposes few or weak assumptions on $$ \theta{}$$. This is an example of a proper, uninformative prior.
- Proper prior p.m.f. is one that sums/integrates to unity on its domain, e.g. the constant prior density $$ p(\theta{}) = 1_{(a,b)}(\theta{}) $$ can be made proper on a bounded interval (but is not possible on the full real line).
- Improper priors can still be used for convenience if the results posterior is proper (and sensible).
- Informative priors impose strong constraints on $$ \theta{} $$, based on existing knowledge of epistemic uncertainty, e.g. from previous interferences or educated guesses. This may however introduce bias.
- An uninformative prior has minimal effects on the posterior (the assumption here being the weakness of constraints), but can lead to nonsensical results.
- A weakly informative prior can be a practical middle ground, e.g. add information to uninformative prior, or uncertainty to informative prior.
Harold Jeffreys suggest a general principle for constructing an uninformative prior given some data distribution, such that that prior remains invariant under variable transformation. This uses the Fisher information (how informative/sensitive $$x$$ is about $$\theta{} $$), below given the one-variable version (the following line is equivalent if the log is twice-differentiable),
\begin{align} I(\theta{}) &:= E\left[ \left(\frac{\partial{}}{\partial{}\theta{}} \ln{p(x|\theta{})}\right)^2 \middle| \theta{} \right] = -E\left[ \frac{\partial{}^2}{\partial{}\theta{}^2} \ln{p(x|\theta{})} \middle| \theta{} \right] \end{align}
The Jeffreys prior is stated thus,
$$$$ p(\theta{}) :\propto{} \sqrt{\text{det} I{}(\theta{})} $$$$
Jeffreys prior is equivariant under transformation
Jeffreys prior of the binomial model
We introduce the concept of conjugate priors, which when applied yields a posterior of the same form. This helps to simplify analytical computation. For the binomial distribution, the likelihood is,
$$$$ L(\theta{}|x) \propto{} \theta{}^x (1-\theta{}^{(n-x)}) $$$$
while the conjugate prior is the beta distribution with arbitrary a and b,
$$$$ \pi{}(\theta{}) = \text{Beta}(\theta{}|a,b) \propto{} \theta{}^{(a-1)} (1-\theta{}) ^{(b-1)} $$$$
Interpretation of beta conjugate prior
The beta conjugate prior admits a useful interpretation as the prior observation of $$a-1$$ successes and $$b-1$$ failures. The mean is
\begin{align} E[\theta{}|x] = \frac{x+a}{n+a+b} \rightarrow \begin{cases} \frac{x}{n}, &n,x \gg a,b\;(\text{more data}) \\ \frac{a}{a+b}, &n,x \ll a,b \;(\text{less data}) \end{cases} \end{align}
and the variance is
\begin{align} \text{Var}[\theta{}|x] = \frac{E[\theta|x] (1 - E[\theta|x])}{n+a+b+1} \rightarrow{} 0, \qquad{}n,(a+b)\rightarrow{}\infty \end{align}
Week 1.2 Bayesian Statistics
(pg.12-21)
Bayes' theorem is essentially an extension of the statement of conditional probabilities:
$$$$ p(\theta|x) = \frac{p(x|\theta)p(\theta)}{p(x)} $$$$
There is a reason for this particular form:
- We want to draw conclusions on the likely value of the estimand(s) $$\theta$$, given that we have previously drawn said samples/observations $$x$$. This is denoted as the posterior distribution.
- This is obtained by having some prior assumption of the distribution of $$\theta$$ (known as the prior $$\pi{}(\theta{})$$), which can be as strong as desired.
- e.g. the temperature of a midday in July can be described as a non-negative temperature (weaker), or as a normally distributed value centered at 32degC with a deviation of 1degC (stronger).
- The likelihood provides the (forward) probability that the observation $$x$$ was seen for a given $$\theta{}$$, which can be denoted as $$L(\theta|x)$$.
- The evidence $$Z:=p(x)$$ is the normalizing factor for $$p(\theta|x)$$, and is sometimes called the prior predictive distribution.
- Another name is the marginal likelihood (probability of sample observation). This is not as critical since it ideally can be derived via normalization.
In Bayesian statistics, we can thus summarize succinctly:
$$$$ p(\theta|x) \propto{} L(\theta|x)\pi(\theta) $$$$
Predictions of observables $$\tilde{x}$$ can also be made by extending the posterior,
$$$$ p(\tilde{x}|x) := \int{} d\theta{} \;p(\tilde{x}|\theta{}) p(\theta{}|x) $$$$
Week 1.1 Preliminaries
(pg.1-11)
Main points:
- Exchangeability of observations
- Conditionals vs marginals
- Covariance matrix generalization
- Transformation of probability distributions
- Uncertainty as either aleatoric (intrinsic randomness) or epistemic (lack of knowledge)